1．一线膨胀系数为α的正立方体物块，当膨胀量较小时，其体膨胀系数等于（    ）

（A）α          （B）α^1/3              （C）α³         （D）3α

【答案】

D

 

2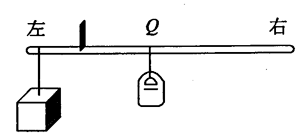．按如下原理制作一杆可直接测量液体密度的秤，称为密度秤，其外形和普通的杆秤差不多，装秤钩的地方吊着一体积为1cm³的较重的合金块，杆上有表示液体密度数值的刻度，当秤砣放在Q点处时秤杆恰好平衡，如图所示。当合金块完全浸没在待测密度的液体中时，移动秤砣的悬挂点，直至秤杆恰好重新平衡，便可直接在杆秤上读出液体的密度，下列说法中错误的是（    ）

（A）密度秤的零点刻度在Q点

（B）秤杆上密度读数较大的刻度在较小的刻度的左边

（C）密度秤的刻度都在Q点的右侧

（D）密度秤的刻度都在Q点的左侧

【答案】

C

 

3．一列简谐横波在均匀的介质中沿x轴正向传播，两质点P₁和P₂的平衡位置在x轴上，它们相距60cm，当P₁质点在平衡位置处向上运动时，P₂质点处在波谷位置，若波的传播速度为24m/s，则该波的频率可能为（    ）

（A）50Hz           （B）60Hz           （C）400Hz          （D）410Hz

【答案】

AD

 

4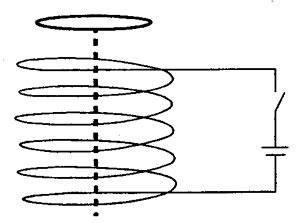．电磁驱动是与炮弹发射、航空母舰上飞机弹射起飞有关的一种新型驱动方式，电磁驱动的原理如图所示，当直流电流突然加到一固定线圈上，可以将置于线圈上的环弹射出去。现在同一个固定线圈上，先后置有分别用铜、铝和硅制成的形状、大小和横截面积均相同的三种环；当电流突然接通时，它们所受到的推力分别为F₁、F₂和F₃。若环的重力可忽略，下列说法正确的是（    ）

（A）F₁＞F₂＞F₃                             （B）F₂＞F₃＞F₁

（C）F₃＞F₂＞F₁                             （D）F₁＝F₂＝F₃

【答案】

A

 

5．质量为m_A的A球，以某一速度沿光滑水平面向静止的B球运动，并与B球发生弹性正碰。假设B球的质量m_B可选取为不同的值，则（    ）

（A）当m_B＝m_A时，碰后B球的速度最大

（B）当m_B＝m_A时，碰后B球的动能最大

（C）在保持m_B＞m_A的条件下，m_B越小，碰后B球的速度越大

（D）在保持m_B＜m_A的条件下，m_B越大，碰后B球的动量越大

【答案】

BCD

 

6．用国家标准一级螺旋测微器（直标度尺最小分度为0.5mm，丝杆螺距为0.5mm，套管上分为50格刻度）测量小球直径。测微器的初读数如图（a）所示，其值为______mm，测量时如图（b）所示，其值为____mm，测得小球直径d＝_______mm。

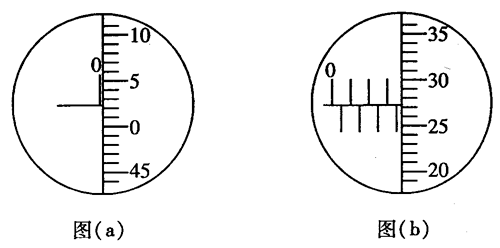
【答案】

0.022～0.024，3.772～3.7743.748～3.752

【解析】

无

 

7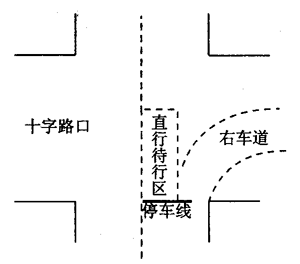．为了缓解城市交通拥堵问题，杭州交通部门在禁止行人步行的十字路口增设“直行待行区”（行人可从天桥或地下过道过马路），如图所示，当其他车道的车辆右拐时，直行道上的车辆可以提前进入“直行待行区”；当直行绿灯亮起时，可从“直行待行区”直行通过十字路口，假设某十字路口限速50km/h，“直行待行区”的长度为12m，从提示进入“直行待行区”到直行绿灯亮起的时间为4s。如果某汽车司机看到上述提示时立即从停车线由静止开始匀加速直线运动，运动到“直行待行区”的前端虚线处正好直行绿灯亮起，汽车总质量为1.5t，汽车运动中受到的阻力恒为车重的0.1倍。则该汽车的行驶加速度为______m/s²；在这4s内汽车发动机所做的功为______J（重力加速度大小取10m/s²）

【答案】

1.5；4.5×10⁴

 

8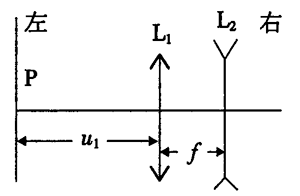．如图所示，两个薄透镜L₁和L₂共轴放置。已知L₁的焦距f₁＝f，L₂的焦距f₂＝－f，两透镜间的距离也是f，小物体位于物面P上，物距u₁＝3f。

（1）小物体经过这两个透镜成的像在L₂的_____边，到L₂的距离为_______，是______像（填“实”或“虚”）、_______像（填“正”或“倒”），放大率为__________。

（2）现把两个透镜位置调换，若还要使给定的原物体在原像处成像，两透镜作为整体应沿光轴向_______边移动距离_________。这个新的像是_____像（填“实”或“虚”）、_____像（填“正”或“倒”），放大率为_______。

【答案】

（1）右，f，实，倒，1

（2）左，2f，实，倒，1

 

9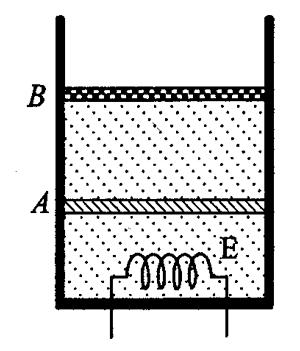．图中所示的气缸壁是绝热的。缸内隔板A是导热的，它固定在缸壁上。活塞B是绝热的，它与缸壁的接触是光滑的，但不漏气。B的上方为大气。A与B之间以及A与缸底之间都盛有n mol的同种理想气体。系统在开始时处于平衡状态，现通过电炉丝E对气体缓慢加热。在加热过程中，A、B之间的气体经历____过程，A以下气体经历____过程；

气体温度每上升1K，A、B之间的气体吸收的热量与A以下气体净吸收的热量之差等于_____。已知普适气体常量为R。

【答案】

等压；等容；nR

 

10．宇宙空间某区域有一磁感应强度大小为B＝1.0×10^-9T的均匀磁场，现有一电子绕磁力线做螺旋运动。该电子绕磁力线旋转一圈所需的时间间隔为____s；若该电子沿磁场方向的运动速度为1.0×10^-2c（c为真空中光速的大小），则它在沿磁场方向前进1.0×10^-3光年的过程中，绕磁力线转了_____圈，已知电子电荷量为1.60×10^-19C，电子质量为9.11×10^-31kg。

【答案】

3.6×10^-2；8.8×10⁷

 

11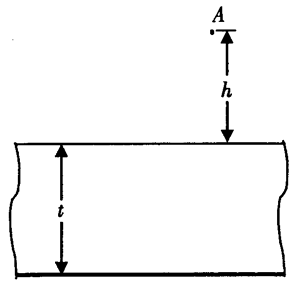．如图所示，一水平放置的厚度为t折射率为n的平行玻璃砖，下表面镀银（成反射镜）。一物点A位于玻璃砖的上方距玻璃砖的上表面为h处。观察者在A点附近看到了A点的像，A点的像到A点的距离等于多少？不考虑光经玻璃砖上表面的反射。

【答案】

如图所示，一水平放置的厚度为t折射率为n的平行玻璃砖，下表面镀银（成反射镜）。一物点A位于玻璃砖的上方距玻璃砖的上表面为h处。观察者在A点附近看到了A点的像，A点的像到A点的距离等于多少？不考虑光经玻璃砖上表面的反射。

 

12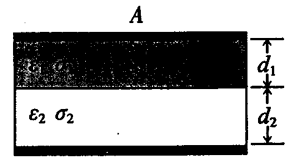．通常电容器两极板间有多层电介质，并有漏电现象。为了探究其规律性，采用如图所示的简单模型。电容器的两极板面积均为A，其间充有两层电介质l和2，第1层电介质的介电常数、电导率（即电阻率的倒数）和厚度分别为ε₁、σ₁和d₁，第2层电介质的则为ε₂、σ₂和d₂。现在两极板加一直流电压U，电容器处于稳定状态。

（1）画出等效电路图；

（2）计算两层电介质所损耗的功率；

（3）计算两介质交界面处的净电荷量；

提示：充满漏电电介质的电容器可视为一不漏电电介质的理想电容和一纯电阻的并联电路。

【答案】

通常电容器两极板间有多层电介质，并有漏电现象。为了探究其规律性，采用如图所示的简单模型。电容器的两极板面积均为A，其间充有两层电介质l和2，第1层电介质的介电常数、电导率（即电阻率的倒数）和厚度分别为ε₁、σ₁和d₁，第2层电介质的则为ε₂、σ₂和d₂。现在两极板加一直流电压U，电容器处于稳定状态。

（1）画出等效电路图；

（2）计算两层电介质所损耗的功率；

（3）计算两介质交界面处的净电荷量；

提示：充满漏电电介质的电容器可视为一不漏电电介质的理想电容和一纯电阻的并联电路。

 

13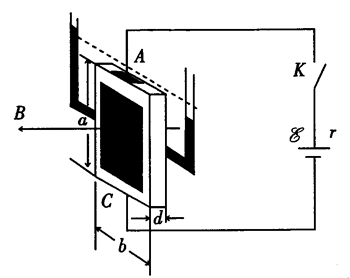．如图所示，一绝缘容器内部为立方体空腔，其长和宽分别为a和b，厚度为d，其两侧等高处装有两根与大气相通的玻璃管（可用来测量液体两侧的压强差）。容器内装满密度为ρ的导电液体，容器上下两端装有铂电极A和C，这样就构成了一个液体电阻。该液体电阻置于一方向与容器的厚度方向平行的均匀恒定的磁感应强度为B的磁场中，并通过开关K接在一电动势为E、内阻为r的电池的两端。闭合开关，若稳定时两侧玻璃管中液面的高度差为h，求导电液体的电导率σ。重力加速度大小为g。

【答案】

σ＝\(\frac{{\rho gha}}{{b(B\varepsilon  - r\rho ghd)}}\)

 

14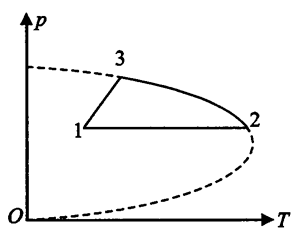．1mol的理想气体经历一循环过程1—2—3—1，如p-T图示所示．过程1—2是等压过程，过程3—1是通过p-T图原点的直线上的一段，描述过程2—3的方程为 

c₁p²＋c₂p＝T

式中c₁和c₂都是待定的常量，p和T分别是气体的压强和绝对温度。已知，气体在状态1的压强、绝对温度分别为p₁和T₁，气体在状态2的绝对温度以及在状态3的压强和绝对温度分别为T₂以及p₃和T₃。气体常量R也是已知的。

（1）求常量c₁和c₂的值；

（2）将过程1—2—3—1在p-V图示上表示出来；

（3）求该气体在一次循环过程中对外做的总功。

【答案】

1mol的理想气体经历一循环过程1—2—3—1，如p-T图示所示．过程1—2是等压过程，过程3—1是通过p-T图原点的直线上的一段，描述过程2—3的方程为 

c₁p²＋c₂p＝T

式中c₁和c₂都是待定的常量，p和T分别是气体的压强和绝对温度。已知，气体在状态1的压强、绝对温度分别为p₁和T₁，气体在状态2的绝对温度以及在状态3的压强和绝对温度分别为T₂以及p₃和T₃。气体常量R也是已知的。

（1）求常量c₁和c₂的值；

（2）将过程1—2—3—1在p-V图示上表示出来；

（3）求该气体在一次循环过程中对外做的总功。

 

15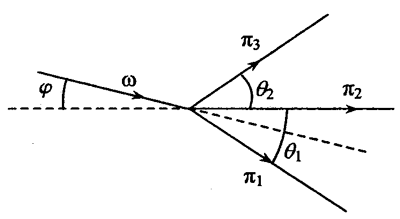．一个ω介子飞行时衰变成静止质量均为m的三个π介子，这三个π介子的动量共面。已知：衰变前后介子运动的速度都远小于光在真空中的速度c；衰变后的三个π介子的动能分别为T₁、T₂和T₃，且第一、二个π介子飞行方向之间的夹角为θ₁，第二、三个π介子飞行方向之间的夹角为θ₂（如图所示）；介子的动能等于介子的能量与其静止时的能量（即其静止质量与c²的乘积）之差。求ω介子在衰变前的瞬间的飞行方向（用其飞行方向与衰变后的第二个介子的飞行方向的夹角即图中的φ角表示）及其静止质量。

【答案】

φ＝arctan\(\frac{{\sqrt {{T_1}} \sin {\theta _1} - \sqrt {{T_3}} \sin {\theta _2}}}{{\sqrt {{T_1}} \cos {\theta _1} + \sqrt {{T_2}}  + \sqrt {{T_3}} \cos {\theta _2}}}\)

p_ω² ＝2m（T₁＋T₂＋T₃）＋4m[\(\sqrt {{T_1}{T_3}} \)cos（θ₁＋θ₂）＋\(\sqrt {{T_1}{T_2}} \)cosθ₁＋\(\sqrt {{T_2}{T_3}} \)cosθ₂]

m_ω＝\(\frac{3}{2}\)m＋\(\frac{1}{{2{c^2}}}\)（T₁＋T₂＋T₃）＋\(\sqrt {{{[\frac{3}{2}m + \frac{1}{{2{c^2}}}({T_1} + {T_2} + {T_3})]}^2} - \frac{{p_\omega ^2}}{{2{c^2}}}} \)

 

16．一圆盘沿顺时针方向绕过圆盘中心O并与盘面垂直的固定水平转轴以匀角速度ω＝4.43rad/s转动。圆盘半径r＝1.00m，圆盘正上方有一水平天花板。设圆盘边缘各处始终有水滴被甩出，现发现天花板上只有一点处有水。取重力加速度大小g＝9.80m/s²。求

（1）天花板相对于圆盘中心轴O点的高度；

（2）天花板上有水的那一点的位置坐标。

【答案】

（1）y_1max＝1.25m

（2）y轴与天花板的交点为天花板上有水的那一点的位置，其坐标值为（0，1.25m）。

【解析】

一圆盘沿顺时针方向绕过圆盘中心O并与盘面垂直的固定水平转轴以匀角速度ω＝4.43rad/s转动。圆盘半径r＝1.00m，圆盘正上方有一水平天花板。设圆盘边缘各处始终有水滴被甩出，现发现天花板上只有一点处有水。取重力加速度大小g＝9.80m/s²。求

（1）天花板相对于圆盘中心轴O点的高度；

（2）天花板上有水的那一点的位置坐标。