1．传感器

传感器是一种检测装置，能将感受到的信息按照一定规律转变为电信号或其他所需形式的信息输出。

 

1．力传感器的敏感元件是悬臂梁和应变片，如图所示是其内部原理示意图。悬臂梁左侧固定，右侧为受力端，其上下表面分别固定两个完全相同的电阻应变片 A、B。当受力端受到一个竖直向下的外力作用时，悬臂梁发生微小形变，导致 A、B 的电阻发生变化。则

（1）应变片 A 的长度________（选填“变长”、“不变”或“变短”）。

（2）两应变片的电阻变化情况是（    ）

A．R_A 变大，R_B 不变                   B．R_A 变大，R_B 变小

C．R_A 变小，R_B 变大                   D．R_A 变大，R_B 变大

 

2．分体式位移传感器是由发射器和接收器组成。如图（a）所示，工作时发射器同时向接收器发射一个红外线和超声波脉冲信号，其中属于电磁波的是__________。接收器接收到脉冲信号后通过计算机算得两者间的距离。若某次测量中发射器和接收器均保持静止，脉冲信号发射与接收的时间分别如图（b）、（c）所示。已知超声波在空气中的传播速度为 v，则发射器离接收器的距离为_______。

 

3．手机的环境光传感器能感知环境光强，其核心元件是光敏电阻 R_G，R_G 的阻值会随光照强度的增大而减小，从而实现自动调节屏幕亮度。

（1）光敏电阻的外壳通常有一层透明材料保护层，以达到既透光又能保护内部光敏元件的效果。如图是一个简化模型。若一束光入射时与保护层表面的夹角为 α，进入保护层后折射光与表面成 θ 角，则该透明保护层的折射率为 n =________。如果改变入射角大小，在该界面上能否发生全反射？________（选填“能”或“不能”）

（2）将一光敏电阻 R_G 与定值电阻 R₁、R₂ 及电源连接成图所示闭合电路．当环境光强增大时，电路中（    ）

A．电流表 A 示数增大

B．电压表 V₁ 示数增大

C．电压表 V₂ 示数增大

D．电源消耗总功率减小

【答案】

1．（1）变长          （2）B

2．红外线；v(t₂ – t₁)

3．（1）（或）；不能               （2）C

 

2．振动的研究

某同学利用如图所示的力传感器研究简谐运动过程。弹性良好的轻质弹簧上端固定一力传感器，下端连接一定质量的钩码。取钩码处于静止状态时位置为坐标原点、向上为正方向建立坐标轴。

 

1．将钩码向下拉动至 − 20 cm 处后静止释放，则在钩码从释放位置至第一次到达平衡位置的过程中，钩码（    ）

A．处于超重状态，减小的弹性势能等于增加的动能

B．处于超重状态，减小的弹性势能大于增加的动能

C．处于失重状态，减小的弹性势能等于增加的动能

D．处于失重状态，减小的弹性势能大于增加的动能

 

2．如图所示是该同学通过实验得到的力传感器的示数随时间变化的曲线，由此推断钩码

（1）在 t₀ 时刻加速度 a₁ 和在 2t₀ 时刻加速度 a₂ 的关系是（    ）

A．a₁ = a₂，方向相反

B．a₁ = a₂，方向相同

C．a₁ < a₂，方向相反

D．a₁ < a₂，方向相同

（2）振动过程中其位移–时间图像应当是（    ）

【答案】

1．B

2．（1）A               （2）C

 

3．力学研究

如图为某创新实验室制作的一个“圆环轨道力学装置”示意图。其中直轨道 AB 与光滑竖直半圆轨道 BCD 平滑连接，直径 BD 处于竖直方向，C 点位于圆心等高处一小球经固定的弹簧发射器发射出后，沿直轨道运动，经 B 点沿半圆轨道上升，并从 D 点水平抛出，最后落在轨道 AB 上。已知小球质量为 m = 0.5 kg，半圆轨道半径 R = 0.4 m，安装于 D 处的光电门测得速度 v_D = 3 m/s。重力加速度为 g = 10 m/s²。（不考虑空气阻力）

 

1．小球从 A 点弹出时获得的动能由____________能转化而来。运动到 B 点时发现速度有所减小，可能的原因是_______________________________。

 

2．（多选）小球沿 BCD 轨道上升过程中，小球（    ）

A．在 D 点时加速度方向向下

B．在 C 点时加速度方向向左

C．从 B 到 D 的过程中，只有重力做功

D．从 B 到 D 的过程中，支持力先做正功后做负功

 

3．小球从 B 点到达 D 点的过程中，其速度大小 v_t 与其离 B 点的竖直高度 h 的关系，下列 v_t–h 图可能正确的是（     ）

4．计算：①若 AB 轨道水平，则小球从 D 点抛出后，落地点距 B 点距离 s；

②当小球在 B 点速度小于多少时，将无法到达 D 点？

【答案】

1．弹性势；AB 轨道粗糙，小球克服摩擦力做功（或 AB 轨道斜向右上）

2．AC

3．D

4．（1）s = 1.2 m

（2）v_B = 2\(\sqrt 5 \) m/s = 4.47 m/s

 

4．手摇起电机

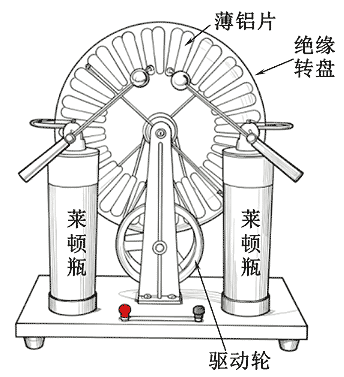手摇起电机是教学中产生静电的重要装置。它由粘有薄铝片的绝缘转盘、莱顿瓶、电刷、集电针等零件构成，如图是其结构示意图。

 

1．静电的产生有接触起电、感应起电和摩擦起电等方式。其中摩擦起电过程中，如果有 P、Q 两物体发生摩擦，使得 P 带上了正电。则（    ）

A．质子从 P 转移到 Q                 B．质子从 Q 转移到 P

C．电子从 P 转移到 Q                 D．电子从 Q 转移到 P

 

2．通过如图所示简述感应起电原理。A、B 是绝缘转盘上粘贴的一对薄铝片，如先将一正电荷靠近铝片 A，稳定后，A 的右端带______（选填“正电”、“负电”或“不带电”）。此时再用导线将 A 和 B 连接，稳定后再移除导线，此后铝片 B 带________（选填“正电”、“负电”或“不带电”）。

 

3．若与两个莱顿瓶相连的金属小球 A、B 的直径为 1 cm，分别带上 q = 1×10⁻⁷ C 的等量异种电荷，如图所示。

（1）当两金属球逐渐靠近的过程中，两球间的电场强度将________（选填“增大”、“减小”、“不变”），两球电势能将________（选填“增大”、“减小”、“不变”）。

（2）当距离减小到 d = 2 cm 时，出现空气被电离击穿而形成火花放电现象。若此时两球间电压 U_AB = 6×10⁴ V。小崇同学用所学的知识，求出了此时两金属球间的电场强度。请对其求解过程做简要评价，说明结论正确与否，并说明理由。

根据电场强度公式：E = \(\frac{{{U_{{\rm{AB}}}}}}{d}\) = \(\frac{{6 \times {{10}^4}}}{{2 \times {{10}^{ - 2}}}}\) N/C = 3.0×10⁶ N/C

答：是否正确________，理由：________________________________________________。

 

4．在研究电容器电容特性时，将两个靠近且彼此绝缘的平行金属板 A、B 组成一个平行板电容器。让两个极板分别与验电器的金属球和外壳相连，验电器指针的偏转角可以定性地反映两极板间的电势差 U 的大小。用起电机给两极板充电后断开，保持极板上电荷量 Q 不变。按如图（a）所示，保持极板 A 不动，向左移动极板 B，增大极板间距离，则电容器电容 C 会________（选填“增大”、“减小”、“不变”）；按如图（b）所示，将 B 板向上移动一段距离，减小两极正对面积，则验电器的张角将________（选填“增大”、“减小”、“不变”）。

【答案】

1．C

2．正电、正电

3．（1）增大、减小

（2）否（错误）；该公式只适用于匀强电场，本题中电场不能看做匀强电场

4．减小；增大

 

5．验证动量守恒定律

如图所示为验证动量守恒定律的实验装置。将两光电门传感器安置在水平导轨上，导轨上的碰撞小车 A 和 B 分别装有挡光片和弹性圈（或尼龙搭扣）。

 

1．如果一个系统在相互作用过程中系统的总动量保持不变，其条件是__________________。

 

2．第一次实验：将小车装有弹性圈的一端相对，使两车靠近并压缩弹性圈，然后从静止同时释放两小车。

（1）（多选题）实验中，下列哪些因素会影响实验结果（    ）

A．两小车质量是否相等                     B．光电门安装的位置

C．两弹性圈的弹性性能                     D．两小车释放是否同时

（2）实验测得两车上挡光片的宽度均为 d，小车的质量分别是 m_A 和 m_B，相对应的光电门测出的挡光时间分别为 t_A 和 t_B，若两小车碰撞前后动量守恒，其表达式可以表示为________。

 

3．第二次实验：已知 m_A = m_B = 0.4 kg，A 车上挡光片宽度 d = 0.8 cm，B 车不带挡光片，将两车分别装有尼龙搭扣的一端相对，保持 B 车静止，让 A 车以一定的速度向 B 车运动。相碰后两车搭在一起运动。挡光片第一次通过光电门的时间为 t₁ = 0.01 s，相撞后挡光片通过第二个光电门的时间 t₂ = 0.02 s。

计算：（1）该碰撞过程中，A 车受到的冲量 I_A；

（2）通过计算判断碰撞过程中系统的动量是否守恒？ 

【答案】

1．系统所受合外力为零或系统不受外力

2．（1）BD          （2）m_A \(\frac{d}{{{t_{\rm{A}}}}}\) = m_B \(\frac{d}{{{t_{\rm{B}}}}}\) 或（m_A \(\frac{d}{{{t_{\rm{A}}}}}\) − m_B \(\frac{d}{{{t_{\rm{B}}}}}\) = 0）

3．（1）I_A = − 0.16 N·s

（2）动量守恒

【解析】

3．（1）v_A = \(\frac{d}{{{t_1}}}\) = \(\frac{{0.008}}{{0.01}}\) m/s = 0.8 m/s，v_Aʹ = \(\frac{d}{{{t_2}}}\) = \(\frac{{0.008}}{{0.02}}\) m/s = 0.4 m/s 

I_A = Δp = m_A(v_Aʹ − v_A) = 0.4×(0.4 – 0.8) N·s = − 0.16 N·s

（2）碰撞前：p = p_A + p_B = m_Av_A + 0 = 0.4×0.8 N·s = 0.32 N·s

碰撞后：pʹ = p_Aʹ + p_Bʹ = (m_A + m_B) v_A = 0.8×0.4 N·s = 0.32 N·s

因为 p = pʹ，所以动量守恒。

 

6．自行车运动

低碳时代，自行车不仅作为一种重要的交通工具，自行车运动也已经成为一种时髦休闲运动方式。

 

1．如图所示，若某自行车的后车轮半径 R₁ = 0.3 m，固定在轮轴上的飞轮半径 R₂ = 0.04 m，与脚踏板关联的链轮半径 R₃ = 0.12 m。运动员骑行时每秒蹬脚踏板 2 圈，不考虑车轮打滑等传递损耗。

（1）当自行车在水平路面上向右匀速骑行时，其后轮受到地面的作用力 F 的方向可能是（     ）

（2）链轮的角速度 ω₁ =________rad/s；自行车前行速度 v =________m/s。（结果保留 π）

 

2．某智能电动助力自行车在水平平直公路上由静止开始运动，运动过程中各类机械摩擦等损耗可折合成一个恒定的阻力 f₀，其大小为车和人总重力的 0.06 倍（g = 10 m/s²）。已知骑行者与自行车总质量 m = 100 kg。骑行者做了如下的一个实验研究，将工作模式分为二个阶段：

（1）第一阶段：0 ~ 6 s 内电动辅助驱动阶段。电动车从静止开始，骑行者提供沿运动方向恒定牵引力 F₀，同时电动驱动系统提供恒定功率 P₁ = 200 W。3 s 末速度达到最大，且 v_m = 5 m/s。

①该过程中，自行车的加速度变化情况是（    ）

A．一直变大                                          B．先变大后不变

C．一直变小                                          D．先变小后不变

②计算：求人提供的牵引力 F₀ 的大小。

（2）第二阶段：6 s 以后制动减速阶段．骑行者停止施力，自行车在受到阻力 f₀ 的同时，启动了电磁制动模式。通过电磁制动，把部分机械能转化为电能，实现能量回收，直到自行车静止。已知该过程中自行车克服电磁阻力做的功为 W_电 = 650 J。计算：

①第二阶段通过的位移 x₂；

②假设在第一阶段的电动驱动过程中，电源消耗的功率有 75% 转化为驱动系统的输出功率；在能量回收过程中，克服电磁阻力做功有 60% 可以回收为电源能量。则在整个实验过程中，电源储存的能量总共减少了多少？

 

3．电磁制动过程相当于将启动时的电动机变为发电机。如图为一个小型发电机原理图。在磁感应强度为B的匀强磁场中，单匝正方形线圈 abcd 的边长为 L、电阻为 R，绕 OOʹ 轴逆时针（沿 OOʹ 方向看）匀速转动，角速度为 ω。线圈中产生的交流电。

（1）线圈转到图示位置（线圈平面与磁场平行）时，线圈中感应电流方向为__________（选填“abcda”或“adcba”）

（2）此时，线圈中（    ）

A．磁通量最大，感应电动势最小

B．磁通量最大，感应电动势最大

C．磁通量最小，感应电动势最大

D．磁通量最小，感应电动势最小

（3）线圈中交流电的最大值 I_m =_______，在时间 t 内，线圈电阻上产生的热量 Q =_______。

【答案】

1．（1）B             （2）4π、3.6π

2．（1）①D

②F₀ = 20 N

（2）①x₂ = 10 m

②ΔE = 1210 J

3．（1）abcda               （2）C           （3）\(\frac{{B\omega {L^2}}}{R}\)，\(\frac{{{B^2}{\omega ^2}{L^4}t}}{{2R}}\)