十四、研究弹性碰撞

这个实验要研究弹性碰撞中动量守恒和动能守恒。实验装置如图 10–18 所示，让一个小球从斜槽上滚下来，跟放在斜槽末端的另一个质量较小的球发生正碰，测出两球的质量以及它们碰撞前后的速度，就可以研究弹性碰撞中动量和动能是否守恒。

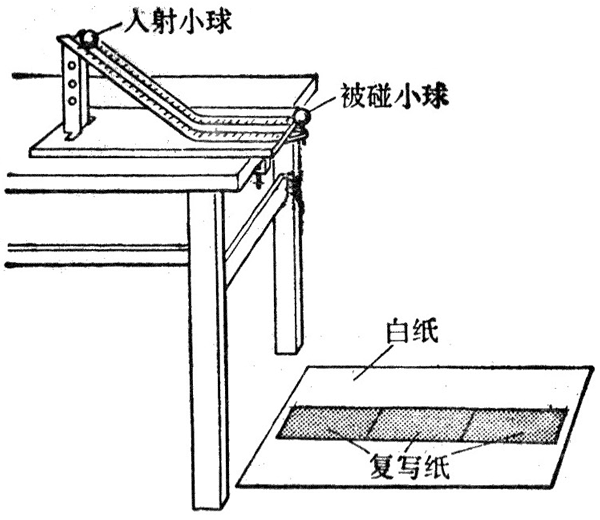
小球的质量可以用天平来测量，怎样测定两球碰撞前后的速度呢？实验时将斜槽固定在桌边，并注意使斜槽的末端点的切线是水平的，被碰小球支在小柱上，两球碰撞时一样高，碰撞前后的速度都是水平的。因此，两球碰撞前后的速度，可以利用我们学过的平抛运动的知识求出来。

做平抛运动的小球下落到地面，它们下落的高度相同，飞行时间也相同，这样，小球的水平速度与其飞出的水平距离成正比，如果用小球的飞行时间作时间单位，小球飞出的水平距离在数值上就等于它的水平速度。

为了记录小球飞出的水平距离，在地上铺一张白纸，白纸上铺放复写纸，小球落在复写纸上，就在白纸上留下小球落地位置的痕迹，利用这个痕迹我们不难测出小球飞出的水平距离。

上面讲了实验装置和实验原理，现在我们做实验。

先不放上被碰小球，让入射小球从斜槽上某一高度滚下，重复 10 次，用尽可能小的圆把所有的小球落点图在里面，圆心 P 就是小球落点的平均位置（图10–19）。

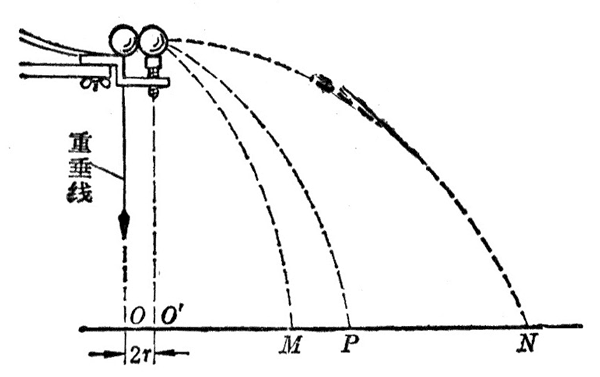
把被碰小球支在小柱上，让入射小球从同一高度滚下，使它们发生正碰。重复 10 次，用同样的办法标出入射小球的落点的平均位置 M、被碰小球的落点的平均位置 N。

现在来测量小球飞出的水平距离。

我们看到实验装置中有个重垂线，它的悬点正好在斜槽的末端点。在白纸上记下重垂线所指的位置 O，它表示斜槽的末端点在纸上的垂直投影。不发生碰撞时入射小球飞出的水平距离应当从斜槽末端点在纸上的垂直投影算起，因此线段 OP 是不发生碰撞时入射小球飞出的水平距离，它在数值上等于入射小球碰擅前的速度 v₁。

支持被碰小球的小柱和斜槽末端点的距离为 2r，其中 r 是两个小球的半径，在直线 ON 上取线段 OOʹ = 2r，则 Oʹ 点就是碰撞时被碰小球的球心在纸上的垂直投影，因此线段 OʹN 是被被小球碰撞后飞出的水平距离，它在数值上等于被碰小球碰撞后的速度 v₂′。

从图 10–19 可以看出，碰撞时入射小球的球心在斜槽末端点的上方，因此线段 OM 是入射小球碰撞后飞出的水平距离，它在数值上等于入射小球碰撞后的速度 v₁′。

测量完毕，我们可以利用测量结果进行研究了。

先研究动量守恒，根据动量守恒定律应当有

\[{m_1}{v_1} = {m_1}{v_1}^\prime  + {m_2}{v_2}^\prime \]

因为 v₁，v₁′，v₂′ 在数值上分别等于线段 OP，OM，O′N 的长度，所以

\[{m_1}(OP) = {m_1}(OM) + {m_2}(O'N)\]

把测得的数据代入上式，看看等式是否成立。

再来研究动能守恒。在弹性碰撞中动能守恒，所以应当有

\[\frac{1}{2}{m_1}v_1^2 = \frac{1}{2}{m_1}v{'}_1^2 + \frac{1}{2}{m_2}v{'}_2^2\]

\[{m_1}{(OP)^2} = {m_1}{(OM)^2} + {m_2}{(O'N)^2}\]

把测得的数值代入上式，看看等式是否成立。

根据实验结果，总结弹性碰撞的规律。

做这个实验的时候，入射小球的质量 m₁ 必须大于被碰小球的质量 m₂。你能利用所学知识来说明其中的道理吗？

在研究弹性碰撞中动能守恒时，也可以不用等式

\[{m_1}{(OP)^2} = {m_1}{(OM)^2} + {m_2}{(O'N)^2}\]

而把测得的数据代入等式 O′N − OM = OP 中，看看它是否成立，就知道动能是否守恒。研究一下这个问题，说明道理，并把你测得的数据代入后一等式，看看它是否成立。

发布时间：2025/11/26 上午7:22:29  阅读次数：162